Range
La sequenza di numeri interi consecutivi è di uso così frequente in Python che è stata definita una funzione specifica, range(), per crearla.
La sintassi:
range (n1, n2, p)
dove
- n1 l'intero da cui iniziare la sequenza; è opzionale e per default è 0
- n2 l'intero, escluso, con cui concludere la sequenza
- p l'incremento (passo) della sequenza; è opzionale e per default è 1
Indipendentemente dall'intervallo che rappresenta, la funzione range() memorizza solo i valori di inizio, fine ed incremento, per cui consuma molto meno memoria di quella che occuperebbe una lista.
Esempio
a= range(3,6)
for x in a:
print(x, end='\t')
Risultato
3 4 5
Esempio
a= range(6)
for x in a:
print(x, end='\t')
Risultato
0 1 2 3 4 5
Esempio
a= range(3,9,2)
for x in a:
print(x, end='\t')
Risultato
3 5 7
� Esercizio
Scrivere un programma che determini i divisori di un numero naturale digitato dall'utente.
Una possibile soluzione
n = int(input("Digita il numero naturale del quale determinare i divisori: "))
print(f"I divisori di {n} sono:")
for i in range(1, n+1): #range(1,n+1) crea una sequenza di numeri da 1a n+1 escluso
if n % i == 0:
print(i, end=' ')
� Esercizio
Visualizzare la tabellina di un numero naturale da 1 a 10 digitato dall'utente
Una possibile soluzione
n = int(input("Digita un numero intero da 1 a 10 del quale visualizzare la tabellina: "))
for i in range(1,11):
print(n * i, end=" ")
� Esercizio
Verificare se il numero naturale digitato dall'utente è un numero primo.
Una possibile soluzione
n = int(input("Digita il numero naturale del quale verificare se è un numero primo: "))
primo = True
for i in range(2, n, 1):
if n%i == 0:
primo = False
if primo:
print(f"Il numero {n} è primo!")
else:
print(f"Il numero {n} non è primo!")
Il 2 non viene preso in considerazione dal ciclo, per cui non altera il contenuto della variabile primo che permane col valore True.
Tale soluzione è volutamente elementare, vedremo nella fase dedicata alla Matematica come ottimizzarla.
Tuple
La tuple è un insieme ordinato di più elementi in un'unica variabile, e fin qui la definizione coincide con quella della lista, ma allora per cosa sono simili e per cosa differiscono?
Le differenze
- Innanzitutto denotiamo la differenza nella loro creazione:
a=[a,b,c,d,e] è una lista
b=(a,b,c,d,e) è una tupla
Una tupla è definita con gli elementi posti fra una parentesi tonda di apertura ed una di chiusura o semplicemente, senza parentesi, scrivendo i suoi elementi separati da virgole (sconsigliato).1
- La differenza fondamentale tra le tuple e le liste è che mentre le prime non possono essere modificate, le seconde sì: cioè le tuple sono oggetti immutabili.
- Fra una tupla ed una lista contenenti gli stessi elementi, la tupla è più efficiente in termini di memoria.
Poiché le liste sono mutabili, Python deve riservare memoria aggiuntiva per consentire, dopo la sua creazione, una eventuale estensione della sua dimensione con l'aggiunta o modifica dei suoi elementi. Differentemente accade per le tuple che hanno dimensione fissa, poiché immutabili, e per le quali Python riserva il minimo della memoria richiesta dai dati. - Per lo stesso motivo anzidetto, le tuple hanno una migliore efficienza temporale, soprattutto nella fase di ricerca
Le similitudini
- Sia nelle tuple che nelle liste è possibile archiviare qualsiasi tipo di dati.
- Sia le tuple che le liste sono ordinate.
- È possibile scorrere gli elementi contenuti sia nelle tuple che nelle liste, poiché sono entrambi tipi di dati sequenziali.
- Si possono effettuare sulle tuple tutte quelle operazioni previste con le liste che non ne prevedano modifiche; in particolare si può accedere sia agli elementi delle tuple che delle liste usando le parentesi quadre e un indice ([indice]).
Per motivi di efficienza, se si hanno dati che non dovrebbero cambiare, è opportuna la scelta del tipo di dati tupla piuttosto che lista.
Oggetti e valori
Se vengono create due diverse variabili alle quali viene assegnato lo stesso valore di tipo lista
var1=['a','b','c','d','e']
var2=['a','b','c','d','e']
e si ricavano i loro identificatori
print(id(var1))
print(id(var2))
140307786079040
140307782128512
si scopre che le liste hanno un comportamento diverso dai dati numerici e le stringhe, due liste diverse fanno SEMPRE riferimento ad oggetti diversi.
Occorre però fare una precisazione; si analizzi il seguente programma:
var1=['a','b','c','d','e']
var2=var1
e si ricavano i loro identificatori
print(id(var1))
print(id(var2))
140091535792960
140091535792960
var1 e var2 si riferiscono allo stesso oggetto (si può dire che sono due alias dello stesso oggetto). Se modifico var1 viene modificato il valore di var2, poiché fanno riferimento allo stesso oggetto; dunque conviene evitare la creazione di un alias ed effettuare una copia che assume un id diverso.
Le matrici (*)
La matrice è una lista annidata i cui elementi sono le liste costituite dagli elementi di una riga. Chiariamo con un esempio. La matrice può essere rappresentata dalla lista annidata di tre elementi
M = [ [1, 2, 3, 4], [5, 6, 7, 8],[9, 10, 11, 12]]
per cui M[0] seleziona la prima riga, M[1] la seconda, M[2] la terza. Per individuare un singolo elemento della matrice si deve usare un doppio indice: il primo per la riga ed il secondo per la colonna; ad esempio
M [2] [2]
individua l'elemento all'incrocio fra la terza riga e la terza colonna, cioè 11.
Va sottolineato che questo è uno dei vari modi di rappresentare le matrici; un'alternativa, ad esempio, è quella di rappresentare la matrice come una lista di colonne invece che di righe.
Attività ludica e di consolidamento con la turtle graphics 2
Le procedure grafiche ben si prestano al consolidamento dei costrutti fin qui appresi, poichè ne consentono un riscontro visivo immediato ed inoltre aprono la strada alla progettazione delle funzioni.
Un aiuto viene dal modulo grafico turtle che consente la creazione di immagini grazie alla turtle graphics3, modulo già integrato in quasi tutte le installazioni di Python.
Il modulo turtle crea una tartaruga, rappresentata simbolicamente nel nostro caso dalla punta di una freccia; durante il movimento, ottenuto con comandi esplicativi e molto semplici, trasporta una penna con la quale può lasciare traccia del suo movimento. Al momento della sua creazione la tartaruga è orientata a destra ed è posta al centro dello schermo che viene individuato come un sistema di assi cartesiani ortogonali il cui punto di origine è proprio il suo centro.
La tartaruga nasce con coordinate (0,0) ed orientata a destra.
Per iniziare a disegnare è ovviamente necessario importare il modulo:
import turtle
che mette a disposizione moltissimi metodi4, i più popolari dei quali vengono riportati nelle seguenti tabelle, raggruppati per omogeneità.
|
Movimento |
Descrizione |
|
forward(pixel) fd(pixel) |
Sposta la tartaruga in avanti, nell'orientamento contestuale, di una distanza pari al numero di pixel specificato come parametro. |
|
backward(pixel) bk(pixel) |
Sposta la tartaruga indietro, nel verso contestuale, di una distanza pari al numero di pixel fornito come parametro. |
|
left(angolo) lt(angolo) |
Ruota in senso antiorario dell'angolo sessagesimale specificato. |
|
right(angolo) rt(angolo) |
Ruota in senso orario dell'angolo sessagesimale indicato. |
|
goto(x,y) |
Sposta la tartaruga nel punto di coordinate (x,y); home (la tana) ha coordinate (0,0). |
|
home() |
Sposta la tartaruga nel punto di coordinate (0,0) cioè al centro dello schermo e la orienta a destra. |
|
reset() |
Dopo aver pulito lo schermo, colloca la tartaruga nel punto di coordinate (0,0) cioè al centro dello schermo e la orienta a destra. Se si vuol pulire lo schermo, lasciando inalterata la posizione della tartaruga è messo a disposizione il metodo clear(). |
|
speed(velocità) |
Imposta la velocità della tartaruga con un argomento intero compreso tra 0 e 10: da 1 a 10 con un'animazione sempre più rapida sia nel disegno delle linee che nella rotazione della tartaruga, mentre con la velocità impostata su 0 tutto avviene con una velocità ancora più alta delle precedenti. |
I primi quattro metodi impartiscono spostamenti relativi, i restanti imprimono spostamenti assoluti.
Va notato che un parametro negativo per forward produce un movimento indietro e non in avanti, cioè opposto alla traduzione letterale del metodo; in maniera analoga si comportano backward, left e right.
Esempio
Disegniamo un quadrato di lato 200 pixel.
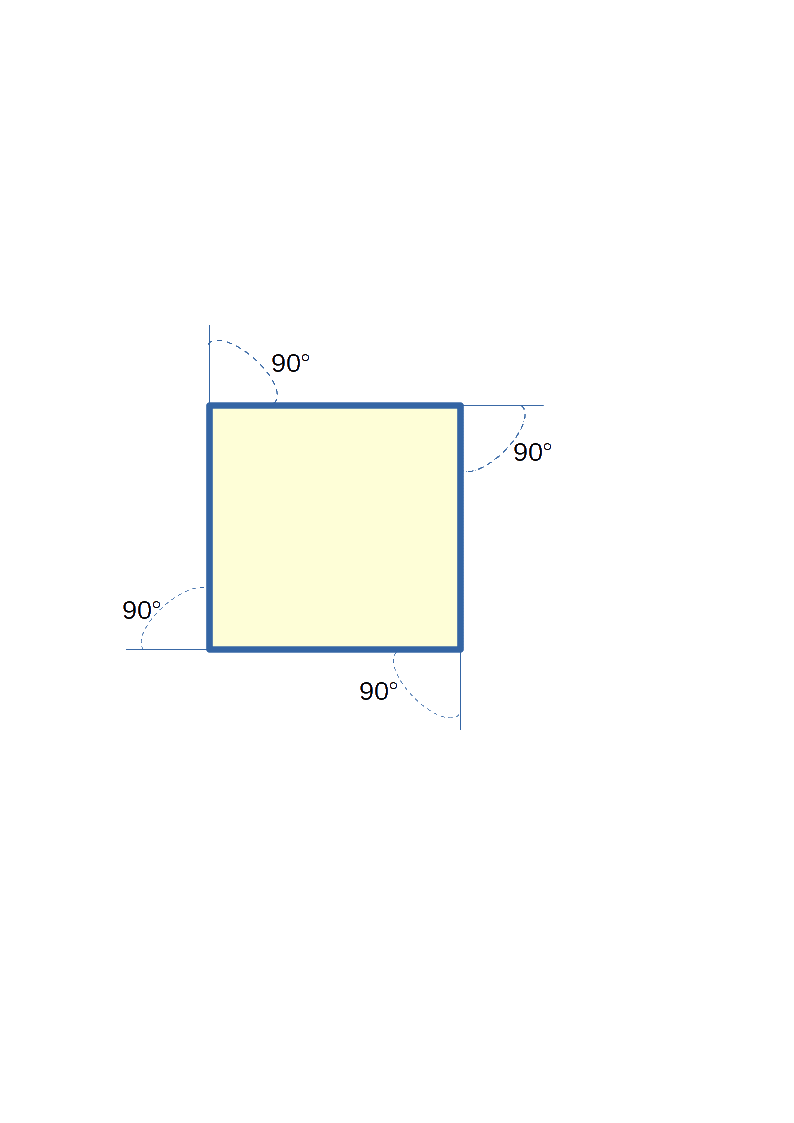
- importare il modulo turtle: import turtle
- mettere giù la penna in modo da lasciare traccia del movimento: turtle.pd()
- muovere la penna in avanti di 200 px: turtle.fd(200)
- ruotare la tartaruga di 90° verso destra (angolo esterno!): turtle.rt(90)
- ripetere l'azione del punto 3
- ripetere l'azione del punto 4
- ripetere l'azione del punto 3
- ripetere l'azione del punto 4
- ripetere l'azione del punto 3
- ripetere l'azione del punto 4 (per portare la tartaruga all'orientamento iniziale)
In definitiva il programma diventa:
import turtle
turtle.fd(200)
turtle.rt(90)
turtle.fd(200)
turtle.rt(90)
turtle.fd(200)
turtle.rt(90)
turtle.fd(200)
turtle.rt(90)
turtle.mainloop()
L'angolo di rotazione della tartaruga è pari all'angolo esterno del lato; poiché, qualunque sia il numero dei suoi lati, la somma degli angoli esterni di un poligono è di 360°, l'angolo di cui la tartaruga deve ruotare è pari a (360/4)°
Mandando in esecuzione il programma si apre la finestra:
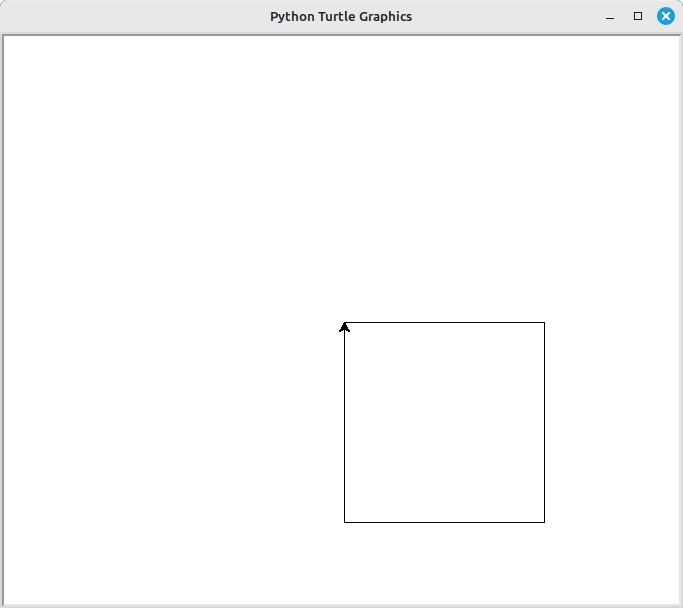
Con il metodo mainloop() il programma attenderà che la finestra grafica della tartaruga venga chiusa.
|
Controllo della penna |
Descrizione |
|
penup() pu() up() |
Solleva la penna; la tartaruga non lascia traccia durante il movimento. |
| pendown() pd() down() |
Abbassa la penna; la tartaruga lascia traccia durante il movimento. |
|
pensize(larghezza) width(larghezza) |
Imposta la larghezza della punta della penna. |
|
pencolor(nomeColore) |
Imposta il colore della penna indicato come stringa: "red", "green", "yellow", "blue", "orange", "gray", "purple", "black", ... |
|
pencolor(r, g, b) |
Imposta il colore della penna sul colore RGB specificando i valori del rosso, verde e blu, con valori fra 0 e 255. |
Esempio
Disegniamo il triangolo avente i vertici nei punti di coordinate A(-50,-70), B(150,20) e C(200,200)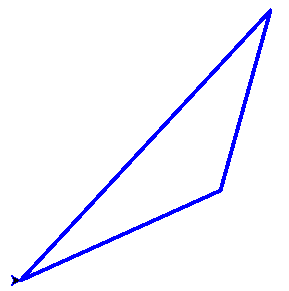
import turtle
turtle.width(4)
turtle.pencolor("blue")
turtle.penup()
turtle.goto(-50,-70)
turtle.pendown()
turtle.goto(150,20)
turtle.goto(200,200)
turtle.goto(-50,-70)
turtle.mainloop()
|
Stato della tartaruga |
Descrizione |
| hideturtle() ht() |
Nasconde la tartaruga. Può essere utile per i disegni complessi, poiché velocizza notevolmente il disegno. |
| showturtle() st() |
Rende visibile la tartaruga. |
| isdown() |
Ritorna |
|
Altri metodi di nostro interesse |
Descrizione |
| bgcolor("colore") |
Personalizza il colore di sfondo della finestra grafica |
| delay(millisecondi) |
Ritarda l'aggiornamento del disegno di un tempo pari ai millisecondi specificati. |
| numinput(titolo,prompt,default,valMin,valMax) |
Apre una finestra di dialogo per l'immissione di un numero. titolo è il titolo della finestra di dialogo prompt è un testo che suggerisce quali informazioni numeriche immettere default è il valore predefinito; opzionale valMin è il minimo del valore da immettere; opzionale valMax è il massimo del valore da immettere; opzionale Se vengono specificati valMin e valMax, il numero da digitare deve essere compreso nell'intervallo da essi individuato, altrimenti viene emesso un messaggio di errore e la finestra di dialogo rimane in attesa di una correzione del dato. Il valore immesso come stringa viene restituito dopo averlo trasformato in float. |
|
circle(raggio) |
Disegna un cerchio del raggio assegnato, partendo della posizione della tartaruga; in senso orario se il raggio è negativo, antiorario se positivo. |
Dare un nome alla tartaruga
Se importiamo il modulo con:
import turtle as tarta
non dovremo più impartire i comandi con riferimento all'oggetto turtle, bensì a tarta; ad esempio per spostare la tartaruga in avanti, scriveremo:
tarta.fd(100)
È possibile pervenire allo stesso risultato creando tarta come una istanza della libreria turtle:
import turtle
tarta=turtle.Turtle()
Va notato che turtle è l'istanza di default.
Quella della creazione delle istanze è una cosa utile laddove si vogliano tracciare più disegni contemporaneamente affidandosi a più oggetti.
Per semplicità nella creazione degli script, nel proseguo importeremo la libreria ponendo in cima al programma la riga
from turtle import *
che ci permetterà di non usare la notazione punto e di scrivere semplicemente il metodo, dando per scontato che essa è riferita all'istanza turtle. ad esempio scriveremo:
fd(200)
invece di turtle.fd(200).
� Esercizio
Come è facile notare, nel tracciare il quadrato viene ripetuta per quattro volte una coppia di comandi: uno di spostamento ed uno di rotazione.
Ottimizzare, con un ciclo for, il codice per disegnare il quadrato di lato 200 px seguendo il seguente programma scritto in linguaggio naturale:
se la penna è su
porta la penna giù
ripeti per 4 volte
avanti 200
ruota a destra di 90°
Una possibile soluzione:
from turtle import *
if (isdown() == False):
pendown
for i in range(4):
fd(200)
rt(90)
mainloop()
Una seconda soluzione:
from turtle import *
n=1
while n<=4:
fd(200)
right(90)
n=n+1
mainloop()
� Esercizio
Creare uno script che disegni un triangolo equilatero di lato 200 px, tenendo presente che ora i lati sono 3 per cui l'angolo esterno è di (360/3)°. Può essere di aiuto il seguente algoritmo in linguaggio naturale:
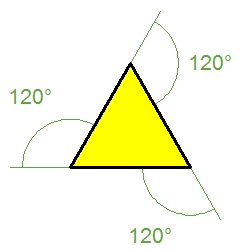
se la penna è su
porta la penna giù
ripeti per 3 volte
avanti 200
ruota a sinistra di (360/3)
Una possibile soluzione:
from turtle import *
if (isdown() == False):
pendown()
for i in range(3):
fd(200)
lt(360/3)
mainloop()
Incapsulamento5
Perché non insegnare alla tartaruga come costruire un quadrato o un triangolo, senza dovergli ripetere i comandi più volte?
Lo possiamo fare definendo una funzione, cioè un insieme di comandi a cui diamo un nome. Ad esempio, se diamo un nome quadrato allo script:
for i in range(4):
fd(200)
lt(360/4)
basterà dire quadrato() alla tartaruga, perché essa tracci un quadrato di lato pari a 200 px. Ad esempio:
from turtle import *
def quadrato():
for i in range(4):
fd(200)
lt(360/4)
if (isdown == False):
pendown()
quadrato()
mainloop()
def sta ad indicare che si sta definendo una funzione; def richiede che accanto, dopo uno spazio, venga indicato il nome che si vuole assegnare alla funzione seguito da una parente tonda aperta, una chiusa e due punti. Subito dopo vanno inseriti i comandi indentati rispetto a def; una riga non indentata pone fine all'incapsulamento.
� Esercizio
![]()
Disegnare 20 quadrati di lato 10 px distanziati fra loro.
Una possibile soluzione:
from turtle import *
def quadrato():
for i in range(4):
fd(10)
lt(360/4)
speed(0)
penup()
goto(-200,0)
hideturtle()
for i in range(20):
pendown()
quadrato()
penup()
forward(20)
mainloop()
_______________________________________________________________
NOTE
1 È possibile creare una tupla costituita da un singolo elemento, purché aggiungiamo una virgola.
2 https://docs.python.org/3/library/turtle.html#starting-a-turtle-environment
3 È un'implementazione del Logo, sviluppato nel 1967 ad opera di Wally Feurzeig, Seymour Papert e Cynthia Solomon.
4 Azioni che può fare.
5 Consiste nell'inglobare una serie di istruzioni in una funzione.

 La nostra Banca di fiducia presso cui puoi farci pervenire le tue donazioni.
La nostra Banca di fiducia presso cui puoi farci pervenire le tue donazioni.